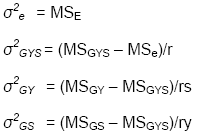Consider a rainfed lowland rice testing program in which the following variances have been estimated in (t/ha)2

 

σ2GE	= 0.30
σ2e	= 0.45

 

The table below shows the predicted effect of the number of trials and replicates of testing on the standard deviation of a cultivar mean:   

 

Number of sites	Number of replicates/ site	S.E. of cultivar mean (t ha-1)	LSD.05 for the difference between cultivar means (t ha-1)
1	1	.87	2.61
	2	.72	2.16
	3	.67	2.01
	4	.64	1.92
2	1	.61	1.83
	2	.51	1.53
	3	.47	1.41
	4	.45	1.35
3	1	.50	1.50
	2	.42	1.26
	3	.39	1.17
	4	.37	1.11
4	1	.43	1.29
	2	.36	1.08
	3	.34	1.02
	4	.32	0.96
5	1	.39	1.08
	2	.32	0.96
	3	.30	0.90
	4	.29	0.87
10	1	.27	0.81
	2	.23	0.69
	3	.21	0.63
	4	.20	0.60

 

Several useful conclusions for planning further testing can be drawn from this table:

 

1. The number of trials is more important than the number of replicates per trial in determining the precision with which cultivar means are estimated.

2. For this testing system (and for many others), there is rarely much benefit from including more than 3 replicates per trial.

3. When the number of trials exceeds 3, there is unlikely to be much benefit to including more than 2 replicates per trial.

 

 

Limitations of the genotype x environment model in resource allocation planning

 

The model set out in Equation 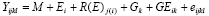has a serious limitation in its usefulness for the planning of testing programs.  In this model, each trial is considered to be a separate environment. It can be used to make decisions about how many replicates are warranted, but it sheds no light on the number of years or locations at which trials should be conducted. However, trials in a MET series are easily and naturally categorized with respect to the year and location in which they were conducted.  

 

If the environment term in Eq. 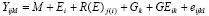is partitioned into year and location effects, a more realistic and informative model can be used for resource allocation exercises, permitting informed decisions to be made about the number of locations, years, and replicates required to achieve an adequate level of precision in cultivar evaluation.

 

 

The genotype x site x year (GSY) model

 

A more realistic and complete model for the analysis of cultivar trials than Eq. 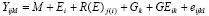recognizes years and sites as random factors used in sampling the TPE.  

 

The resulting model is:

 

 

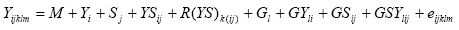
This model differs from the previous Eq. in that the E term has been partitioned into site (S) and year (Y) effects and their interaction (YS).  Similarly, the GE term has been partitioned into GY, GS, and GY components.

 

The variance of a cultivar mean is now expressed as:

 

 

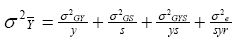
Inspection of this last equation indicates that, if σ2GS  is large, the variance of a cultivar mean can only be minimized if testing is conducted at several sites.  

 

Similarly, if σ2GY is large, testing over several years will be required to achieve adequate precision in the estimation of cultivar means.  However, if  σ2GYS is the largest component of GEI, then it may be possible to minimize 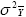   by either increasing the number of sites or the number of years of testing.  

Increasing the number of sites is expensive, but will produce the desired information quickly.  

 

Increasing the number of years of testing is less expensive but will delay cultivar release.  

 

Variance components for the GLY model can also be estimated from the fully balanced ANOVA of a set of trials repeated over locations and years:

 

Table 3.  Expected mean squares (EMS) for the ANOVA of the genotype x location x year (GLY) model assuming all factors random.

 

Source	Mean square	EMS
Years  (Y)
Sites (S)
Y x S
Replicates within Y x S
Genotypes (G)	MSG	σ2e + rσ2GYS + rsσ2GY+ ryσ2GS+ rysσ2G
G x Y	MSGS	σ2e + rσ2GYS +  ryσ2GS
G x S	MSGY	σ2e + rσ2GYS + rsσ2GY
G x Y x S	MSGYS	σ2e + rσ2GYS
Plot residuals	MSe	σ2e

 

 

As for the GE model the variance components for the GLY model can be estimated as functions of the mean squares estimated from the ANOVA: