Example 2: Resource
allocation for a rice breeding program using the GSY model
Cooper et al. (1999) conducted a resource allocation study for the Thai
rainfed lowland rice breeding program in northern Thailand. In
this study over 1000 unselected breeding lines from 7 crosses were evaluated
for 3 years at 8 sites.
Variance components estimates were:
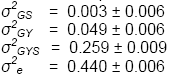
These estimates are of interest in themselves. Their
relative magnitudes yield important information about the nature of GE
interaction in northern Thailand. Inspection
of these estimates leads to the following conclusions:
σ2GS is very small relative
to the other components, indicating that cultivars do not, on average,
perform differently at different locations. There
is little evidence, therefore, that specific lines are adapted to specific
locations within the TPE.
σ2GYS is the largest
component of GEI (a result found in many studies), indicating that cultivar
ranks vary randomly from site to site and from year to year.
σ2eis very large relative
to other components of variance, indicating that within-trial field heterogeneity
is great. High
levels of replication will be needed to achieve acceptable precision.
Improvements
in field technique and the use of experimental designs that control within-block
error should also be considered.
The predicted effect of site, year, and replicate number on the standard
error of a line mean evaluated in northern Thailand is presented below:
The table below shows the effect of location, year and replicate number
on the standard deviation of a cultivar mean: GLY model (variance component
estimates from Cooper et al., 1999):
|
Number of sites |
Number
of years |
Number of replicates/ site |
S.E. of cultivar mean
(t ha-1) |
LSD.05
for the difference betw. cultivar means
(t ha-1) |
|
1 |
1 |
1 |
.87 |
|
|
|
|
2 |
.73 |
|
|
|
|
3 |
.68 |
|
|
|
|
4 |
.65 |
|
|
|
|
|
|
|
|
|
2 |
1 |
.63 |
|
|
|
|
2 |
.54 |
|
|
|
|
3 |
.50 |
|
|
|
|
4 |
.49 |
|
|
|
|
|
|
|
|
5 |
1 |
1 |
.39 |
|
|
|
|
2 |
.33 |
|
|
|
|
3 |
.30 |
|
|
|
|
4 |
.29 |
|
|
|
|
|
|
|
|
|
2 |
1 |
.28 |
|
|
|
|
2 |
.24 |
|
|
|
|
3 |
.23 |
|
|
|
|
4 |
.22 |
|
|
|
|
|
|
|
|
10 |
1 |
1 |
.27 |
|
|
|
|
2 |
.23 |
|
|
|
|
3 |
.21 |
|
|
|
|
4 |
.21 |
|
|
|
|
|
|
|
|
|
2 |
1 |
.20 |
|
|
|
|
2 |
.17 |
|
|
|
|
3 |
.16 |
|
|
|
|
4 |
.15 |
|
Some conclusions:
Testing in approximately
10 trials (5 sites x 2 years or 10 sites x 1 year) is needed to bring
LSD values for the difference between 2 cultivars below 1 ton per ha (the
LSD is approximately 3 times the standard error of a cultivar mean).
Two replicate
per trial are adequate if at least 5 trials are used to estimate means.
Estimates of the variance
of cultivar means from single trials are biased downwards
It is important for breeders to recognize
that the variance of cultivar means estimated from a single trials is
severely biased downwards. This
is because in an analysis of a single trial, there is no way to separate
σ2G from
σ2GY, σ2GS, and σ2GYS.
This is because G, GS, GY, and GYS effects
are completely confounded (or inseparably mixed) in single trials. In
a single trial, only σ2e can be estimated
separately from σ2G and used in the
calculation of the variance of a cultivar mean.
Thus, if the variance of a cultivar mean
is estimated from a in a single trial,
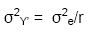
whereas in a MET,
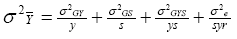
In a single trial, the values of y and s
are 1, and the true variance of a cultivar mean is therefore:
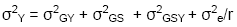
rather than σ2e /r. If
the purpose of the trial is to predict future performance of the varieties
under test, it is clear that σ2Y’
severely underestimates σ2Y.
The literature indicates that the true variance
of a cultivar mean for purposes of prediction is at least twice as large
as the variance estimated from a single
trial. This
is why breeders evaluate advanced lines at several sites.