Breeding theory

2. Randomized complete-block designs

Randomized complete-block designs (RCBDs) group one complete replicate in each block. They are useful when the number of lines in the trial is not large, so that there is less soil and drainage variability within than among blocks. The variability among blocks is thus removed from the plot residuals.   

For complete-block designs, the plot residual term eij  (see 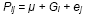) is divided into a complete-block effect R  (also called a replicate effect, since the replicates are synonymous with blocks in the RCBD) and a within-replicate plot residual e.

Thus RCBDs remove effects of blocks from the plot residual, reducing the confounding of genotype with plot residual effects. The model for measurements on a plot is:

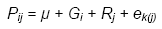
Because all varieties occur in all blocks, the replicate or complete-block effects do not contribute to the SEM (and consequently to the SED and LSD).

3. Incomplete-block designs

When the number of genotypes per replicate is large, there is likely to be great soil heterogeneity even within the block. This variability may be partly controlled by grouping plots within large replicates or complete blocks into much smaller incomplete blocks.  The most commonly-used incomplete-block experimental designs are alpha-lattices for replicated trials and augmented designs  or gridding  for unreplicated trials.  

Models for these designs are more complex than for RCBDs and CRDs, and will not be presented here. In brief, the partitioning of complete blocks into smaller, more homogeneous incomplete blocks permits more of the residual variation among plots to be removed from estimates of genotype means.  

Gridding

Gridding is a simple form of control of residual variation that can be used in unreplicated nurseries, and does not require repeated checks. The nursery is divided into a set of incomplete blocks.  Selection is done within blocks.  

For example, a nursery or unreplicated trial of 500 lines may planted in the field diagrammed below, divided into 5 ranges of 100 lines each.  The field has a toposequence gradient, with the deepest water being in the bottom left and top right corners. If we do not impose any sort of blocking or gridding on the field and we attempt to select the best 20% of the lines on the basis of phenotypic acceptability, we will select mainly from the ends of ranges 1 and 5, which have the deepest water and the latest disappearance of water. We will be selecting mainly on the basis of e, not G.

However, if we divide each range into 5 smaller, more homogeneous blocks of 20 plots each (represented by the dotted lines in the figure below), and select the best 4 lines in each block, we will be selecting the best 20% mainly on the basis of differences in genotypic value rather than water depth.

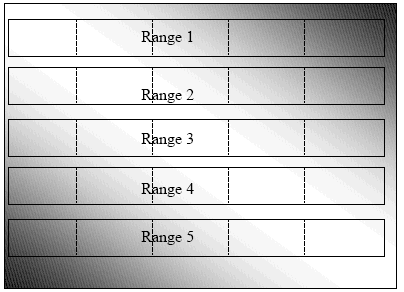
A nursery planted in a field with a toposequence gradient, with 5 ranges of 100 plots each. Dotted lines represent borders of incomplete blocks of 20 plots each.

Augmented designs

Augmented designs also use grids or incomplete blocks to remove some field variation from the plot residuals. In an augmented design, a large set of experimental lines is divided into small incomplete blocks. In each incomplete block, a set of checks is included; every check occurs in each incomplete block, but the experimental lines are included in only one block. Because the design is unreplicated, the repeated checks are used to estimate the error mean square and the block effect. The block effect is estimated from the repeated check means and then removed from the means of the test varieties. This reduces error and increases precision somewhat. However, the repeated checks used to estimate block effects add a substantial number of plots to the trial.  Block effects could also be estimated as effectively from the means of the test varieties in each block. This would save considerable space and labor.

In general, augmented designs have few advantages over unreplicated nurseries in which block effects are estimated without repeated checks.

Alpha-lattice designs

Alpha-lattice designs are replicated designs that divide the replicate into incomplete blocks that contain a fraction of the total number of entries. Genotypes are distributed among the blocks so that all pairs occur in the same incomplete-block in nearly equal frequency. The design permits removal of incomplete-block effects from the plot residuals and maximizes the use of comparisons between genotypes in the same incomplete-block.

How effective are alpha-lattice designs in increasing the precision of genotype means estimated from rainfed rice variety trials? There are several ways to address this question. One way is to compare the SEM or a related statistic like the LSD for trials laid out as alpha-lattices, and analyzed both as alpha-lattices and RCBDs. Surprisingly, there are no published reports of such comparisons in rainfed rice. At IRRI, we have compared the results of alpha-lattice and RCBD analyses for a large set of rainfed lowland breeding lines evaluated at 7 locations in northeast Thailand in the 2001 wet season, as well as for a smaller set of released upland cultivars and advanced lines tested under severe drought stress in 3 different agronomic management regimes in the dry season of 2002. These trials were done in large plots (5 or 6 rows).  We also compared alpha-lattice analysis with RCBD analysis in a 2-replicate trial of 453 lines in an upland drought-stress trial in which single-row plots were used.

The results of these comparisons are presented in the table below.

Table: Comparison of RCBD and alpha-lattice analyses for 7 NE Thailand RL trials (Wet season 2001) and 3 IRRI upland trials (Dry season 2002)

There was little benefit to the alpha-lattice analysis in the trials with fewer entries and larger plots. However, in the upland trial with single-row plots, the benefit of the alpha-lattice block effect removal was great, reducing the standard error of a line mean by nearly half.

In general, alpha-lattice designs are a risk-free way to slightly increase the precision of field trials. It costs no more to conduct an incomplete-block than a complete-block trial.  

Until recently, software that could analyse alpha lattice designs was expensive and usually unavailable to small breeding programs.  

IRRISTAT now supports fast and easy analysis of these trials.

Let's conclude

Summary

1. Replication reduces the influence of plot residuals on cultivar means.

2. Blocking reduces the size of plot residuals by removing the effect of the block.

3. Increasing replication increases repeatability.

4. Alpha-lattices are used to reduce the effect of within-complete-block variation. They can provide risk- and cost-free increases in precision and repeatability, particularly in trials involving very large numbers of entries, and when plot size is small.

5. Augmented designs are suitable for unreplicated nurseries. They distribute test varieties among incomplete blocks that each has a set of common checks. They use many extra check plots, however, and are unlikely to be better than designs where block effects are estimated from the lines in the trial rather than from the repeated checks.

6. Gridding can be used to reduce the effect of soil quality and drainage gradients on selection in unreplicated nurseries