Breeding theory

2. Linear models describing measurements obtained from field trials

The genotype x environment (GE) model

We conduct the combined analysis of variety trials over locations and years within the TPE to estimate the mean performance of varieties. Estimates of the precision of the means (SEM and LSD) are also required. To estimate the variance of a cultivar mean, we must use a statistical model that describes the factors or sources contributing to that variance. The simplest GEI model for the analysis of a MET is:

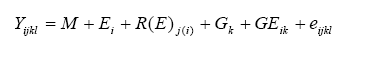
where:

In this model, genotype effects are usually considered fixed; that is, we wish to estimate the performance of the specific genotypes in the trial. Environments and replicates are random factors; we are not interested in the means of the individual trials per se, but rather are interested in them only as sampling the TPE. (Occasionally, genotypes may also be considered random, if the purpose of the trial is to estimate genetic variances rather than to predict cultivar performance.)

GE interactions are random in this model, because the interaction between fixed and random factors is always random. The random GE term contributes to the true error in the test of differences among cultivars, and to the variance of cultivar means.

According to this model, the variance of a cultivar mean is:

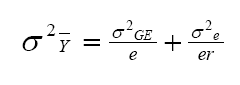
where 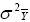  is the variance of a cultivar mean, e is the number of trials, and r is the number of replicates per trial.

It is important to minimize 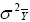  in cultivar testing programs.

Minimizing 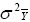  leads to improved prediction of cultivar performance in the future, and increased gains from breeding.

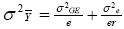can be used to determine the minimum value for  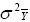  that can be achieved with the resources available to the breeder.  

The variance components can be estimated from the ANOVA table for a completely balanced set of trials (all varieties tested in all trials). Methods for estimating variance components from unbalanced data sets are available but require more sophisticated software.  

The expected mean squares from the ANOVA of a MET are linear functions of the variances of the factors in .  

These are given below:

Table: Expected mean squares (EMS) for the ANOVA of the genotype x environment model assuming all factors random

The variance components can be estimated as functions of the mean squares estimated from the ANOVA:

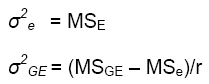
It should be noted that these variance components have very large standard errors, and should be used only as a rough guide to planning a breeding or testing program. They should only be estimated if the number of degrees of freedom for the mean square is about 50 or greater.

Example 1:  Resource allocation for a rice breeding program using the GE model (click on the icon)

Example 2:  Resource allocation for a rice breeding program using the GE model (click on the icon)

Deciding whether to divide a target population of environments into two regions for breeding purposes

The analyses above are useful tools for deciding how many locations, years and replicates of testing are needed to predict performance of a variety with adequate precision. They do not, however, give guidance about whether the TPE should be broken into 2 breeding targets.  

There are many genotype x environment interaction analyses that can be used to group sites into relatively similar groups based on cultivar performance. These methods, including cluster, pattern, and AMMI analyses, are useful when there is no pre-existing hypothesis to test about the pattern of adaptation of varieties to sites.  

However, when there is a good hypothesis to test (based on breeder knowledge, farmer practice, or agroclimatic data), there is a straightforward model that can be used for testing whether locations within the TPE can really be grouped into more homogeneous subsets. In this model, trial sites are grouped into subgroups based on location or some other fixed factor.  

For example, if a breeder wished to evaluate whether two subregions, say the northern and southern parts of the TPE, should be considered separate breeding targets, he or she would classify all trials in the north into one group, and all fields in the south into a second group. A combined analysis would be performed over trials, with the location factor broken down into two subcomponents: subregion  (north or south) and trials within subregion.  

This is illustrated for the 2-way GxE model

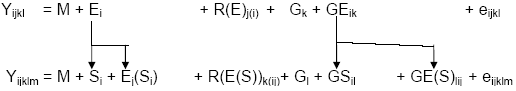
In this model, subregions are considered fixed effects. Locations within subregions are a random sampling factor, like replicates or years. The hypothesis that varieties perform very differently in different regions can be tested by testing the variety x subregion mean square against the variety x locations within subregion mean square. (This model can be easily extended to the genotype x location x year model). Because this is a mixed model the analysis needs to be done with software that can support mixed model analyses, including the latest release of IRRISTAT.

The ANOVA table with expected mean squares for a balanced case is given below:

Table 5.  Expected mean squares (EMS) for the ANOVA of the genotype x subregion for testing fixed groupings of trial sites

Example of a test of significance of genotype x subregion interaction

Breeders in Laos would like to know if the southern and central parts of the country need to be considered separate TPE. A trial involving 22 tradition varieties was conducted at 6 locations in the wet season of 2004, three in the center and three in the south.

The ANOVA table is presented below:

Table: ANOVA for 22 varieties tested in two Lao PDR subregions (north and south), with 3 locations per subregion, in Wet season 2004

In this case, the genotype x subregion (G x S) term is not significant when tested against the pooled genotype x location within subregion (G x L(S)) term.  

Division of this TPE into 2 subregions base on central versus southern location therefore is unwarranted, at least on the basis of this 2004 trial. A combined analysis of an experiment conducted over several years would give a more reliable result.

Let's conclude

Summary

1. The purpose of a variety trial is to predict future performance in the TPE

2. Genotype x environment interaction is large, and reduces the precision with which cultivar means can be estimated.

3. Variance component estimates for the GLY model can be used to develop testing programs that maximize precision for a given level of resources.

4. Within relatively homogeneous TPE, the genotype x site x year variance component is usually the largest. When this is the case, strategies that emphasize either testing over several sites or testing over several years are likely to be successful.

5. Little benefit is obtained from including more than 3 replicates (and often more than 2) in a MET.

6. Standard errors and LSDs estimated from single sites are unrealistically low because they do not take into account genotype x environment interaction

7. A decision about whether a TPE should be split into 2 separate breeding targets can be made by grouping trial sites or locations into subgroupings based on some fixed environmental factor, and then testing the significance of the genotype x  subgroup interaction.

References

Cooper, M., Rajatasereekul, S., Immark, S., Fukai, S., Basnayake, J. 1999b. Rainfed lowland rice breeding strategies for northeast Thailand. I. Genotypic variation and genotype environment interactions for grain yield. Field Crops Research 64: 131-151.  

Atlin, G.N, R.J. Baker, K.B. McRae, and X. Lu.  2000.  Selection response in subdivided target regions.  Crop Sci. 40:7-13.